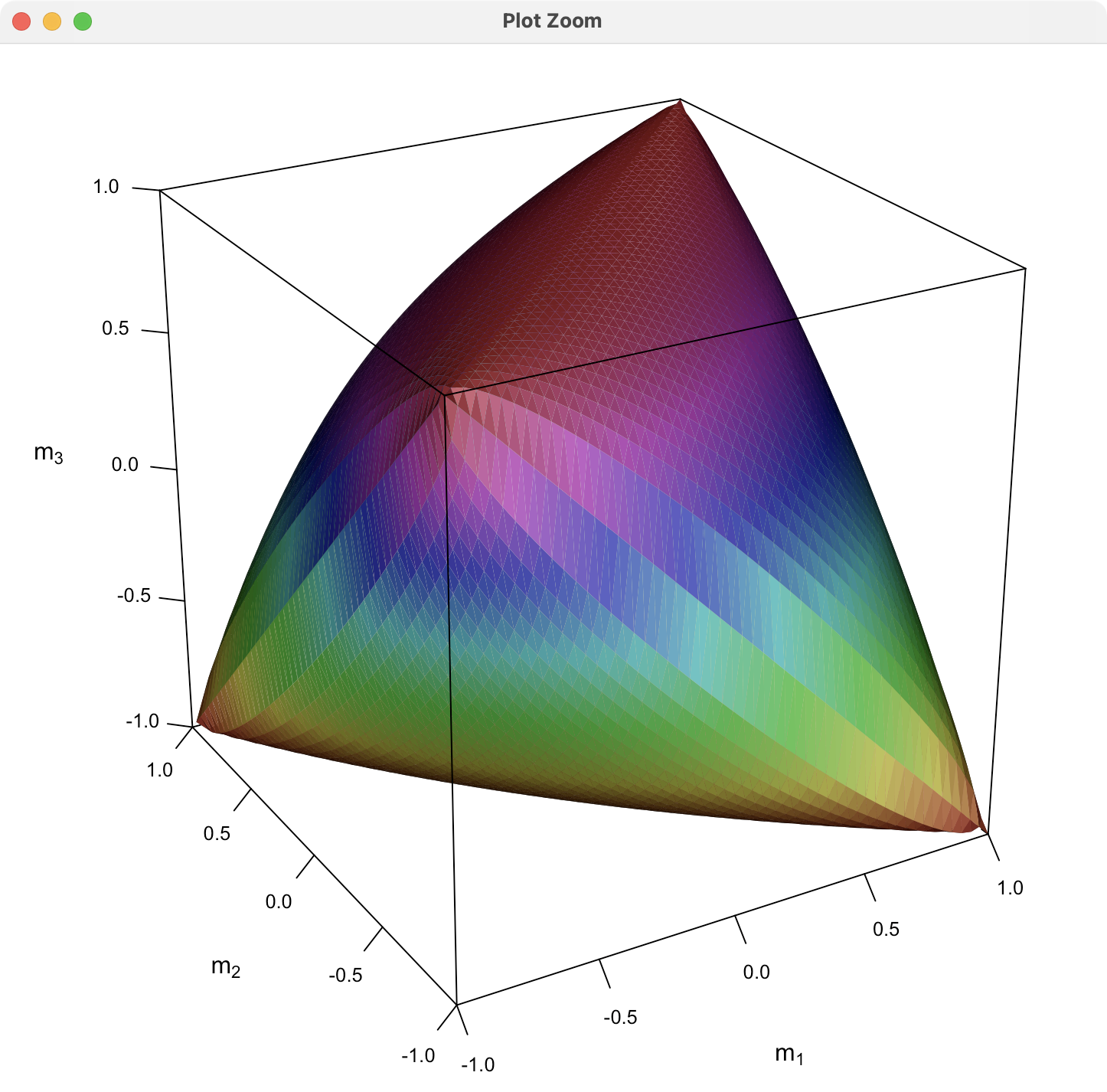
继续按照 fenguoerbian 的思路,用 lattice 包绘制这个图像。代码如下:
# 分两部分绘图
fn1 <- function(x) {
x[1] * x[2] + sqrt(x[1]^2 * x[2]^2 - x[1]^2 - x[2]^2 + 1)
}
fn2 <- function(x) {
x[1] * x[2] - sqrt(x[1]^2 * x[2]^2 - x[1]^2 - x[2]^2 + 1)
}
df1 <- expand.grid(
x = seq(-1, 1, length.out = 51),
y = seq(-1, 1, length.out = 51)
)
df2 <- df1
# 计算函数值
df1$fnxy <- apply(df, 1, fn1)
df2$fnxy <- apply(df2, 1, fn2)
# 添加分组变量
df1$group <- "1"
df2$group <- "2"
# 合并数据
df <- rbind(df1, df2)
library(lattice)
# 自定义调色板
custom_palette <- function(irr, ref, height, saturation = 0.9) {
hsv(
h = height, s = 1 - saturation * (1 - (1 - ref)^0.5),
v = irr
)
}
# 绘图
wireframe(
data = df, fnxy ~ x * y, groups = group,
shade = TRUE, drape = FALSE,
xlab = expression(x[1]),
ylab = expression(x[2]),
zlab = list(expression(
italic(f) ~ group("(", list(x[1], x[2]), ")")
), rot = 90),
scales = list(arrows = FALSE, col = "black"),
shade.colors.palette = custom_palette,
# 减少三维图形的边空
lattice.options = list(
layout.widths = list(
left.padding = list(x = -0.5, units = "inches"),
right.padding = list(x = -1.0, units = "inches")
),
layout.heights = list(
bottom.padding = list(x = -1.5, units = "inches"),
top.padding = list(x = -1.5, units = "inches")
)
),
par.settings = list(axis.line = list(col = "transparent")),
screen = list(z = 30, x = -65, y = 0)
)