使用glmnet包运行LASSO回归:
library(glmnet)
library(dplyr)
library(magrittr)
library(ggplot2)
x <- matrix(rnorm(100*20),100,20) # 自变量矩阵
y <- rnorm(100) #因变量矩阵
fit1 <- glmnet(x,y) # LASSO拟合
plot(fit1,xvar="lambda",label=T) # 回归系数随惩罚项收缩图
lasso.coef <- predict(fit1,type='coefficients',s=0.0656100)[1:20 ,] #提取特定lambda值的模型系数
coeffin <- lasso.coef %>% # 整理数据
as.data.frame() %>%
rename('lasso.coef'='.') %>%
mutate(name=rownames(.)) %>%
filter(lasso.coef<20)
ggplot(coeffin,aes(reorder(name,lasso.coef), # 画出lambda=0.06561时每个变量的系数
lasso.coef)) +
geom_point(size=1.5, color='red')+
coord_flip()+
labs(x='变量',y='LASSO回归系数') +
theme_bw()
运行结果为:
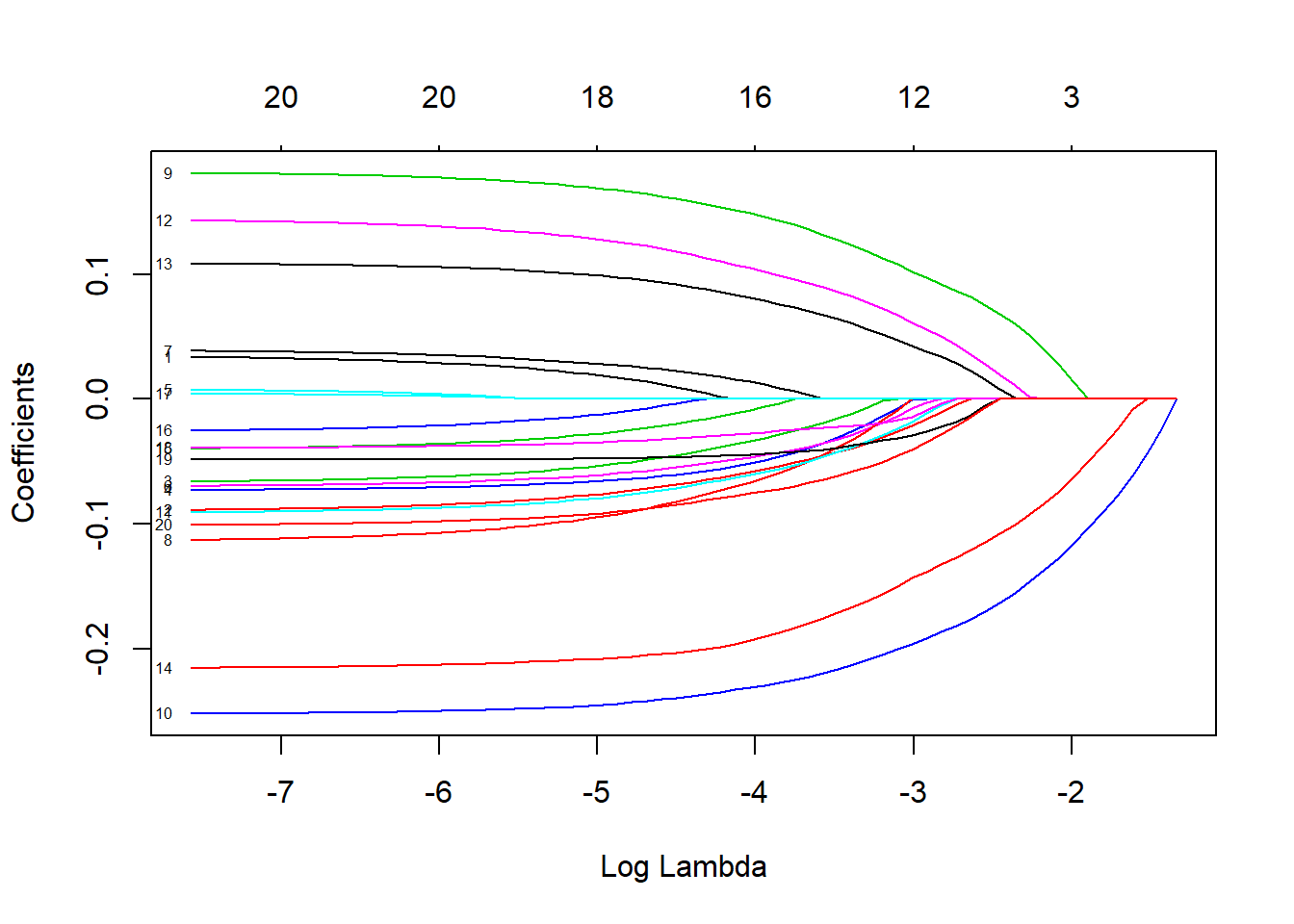
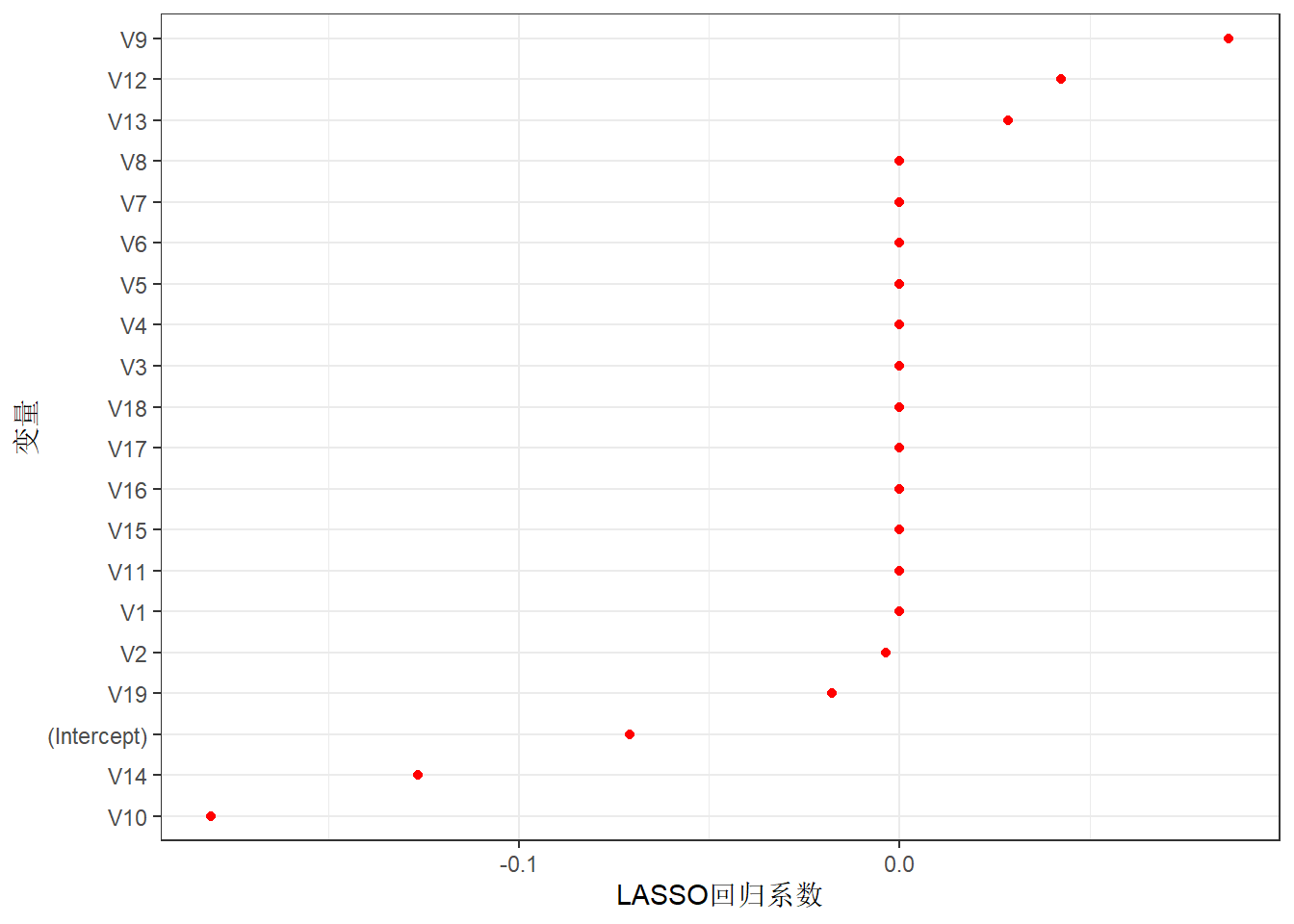
那么图2 显示的系数可以看做各个变量对因变量预测的重要性吗? 因为LASSO事先对自变量进行了无量纲化,是否可以通过系数的比较将最后的结果看做变量的重要性?类似于决策树与随机森林等算法计算的变量重要性那样?
希望和大家讨论下对这个算法的理解。谢谢!