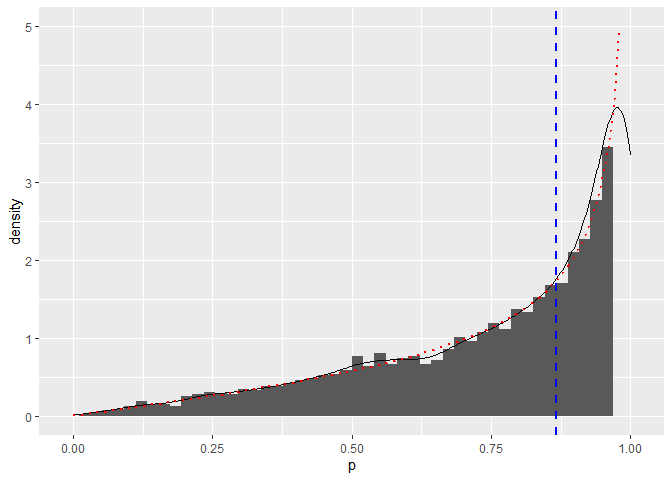
附一个的例子,是要研究一个端点密度趋于无穷的概率分布情况,所以端点的理论曲线会爆掉,需要控制上限。
\(p(x)=\frac{x}{\sqrt{1-x^2}},\quad x\in [0,1]\)
set.seed(42)
x = runif(10000,min=0,max=1)
f = function(x){
sqrt(1-(x-1)^2)
}
p = f(x)
library(ggplot2)
df <- data.frame(
x=x,
p=p
)
ggplot(df, aes(x=p)) +
geom_histogram(aes(y=..density..),bins = 50) +
geom_density(alpha=.2, size=0.7) +
geom_vline(aes(xintercept=sqrt(3)/2),
color="blue", linetype="dashed", size=1)+
geom_function(aes(x=x),fun = function(y){y/(sqrt(1-y^2))},
colour = "red",linetype="dotted", size=1) +
ylim(0,5)
ggplot(df, aes(x=p)) +
geom_histogram(aes(y=..density..),bins = 50) +
geom_density(alpha=.2, size=0.7) +
geom_vline(aes(xintercept=sqrt(3)/2),
color="blue", linetype="dashed", size=1)+
geom_function(aes(x=x),fun = function(y){y/(sqrt(1-y^2))},
colour = "red",linetype="dotted", size=1) +
coord_cartesian(ylim = c(0,5))#不能直接用ylim,以免数据丢失
