
前面简要介绍了一下现代统计模拟方法对于估计参数\(\pi\)的优势。下面就谈谈如何通过Buffon’s Needle的方法进行计算机的模拟,估计出\(\pi\)的值。这里我将使用R语言进行相关程序的编写。
首先要感谢现代计算机的产生,我们不需要真的在一张纸上面扔几千次针来计算针与平行线相交的概率。那么既然我们已经知道了大致估计的思路,如何让计算机去帮我们模拟这过程就成了下一个要解决的问题。虽然计算机不可能帮助我们真的去扔针(貌似买个机器人也能做),但是计算机是可以帮助我们进行快速的判断,什么情况下,针与平行线相交;而什么情况下,针与平行线不相交。如果我有了这个判断条件,再加上我前面已经知晓的公式 \(p = \frac{2L}{\pi D}\),那么我就可以很容易的借助计算机来帮我模拟投针了。这下我想投多少,就可以投多少?而且这里我还可以顺带解决一个问题,到底投多少针,我得到的值才完美呢?
那么如下面的这个图所示,假设\(x\)是针到平行线底部的距离,针与平行线的夹角为\(\theta\)。
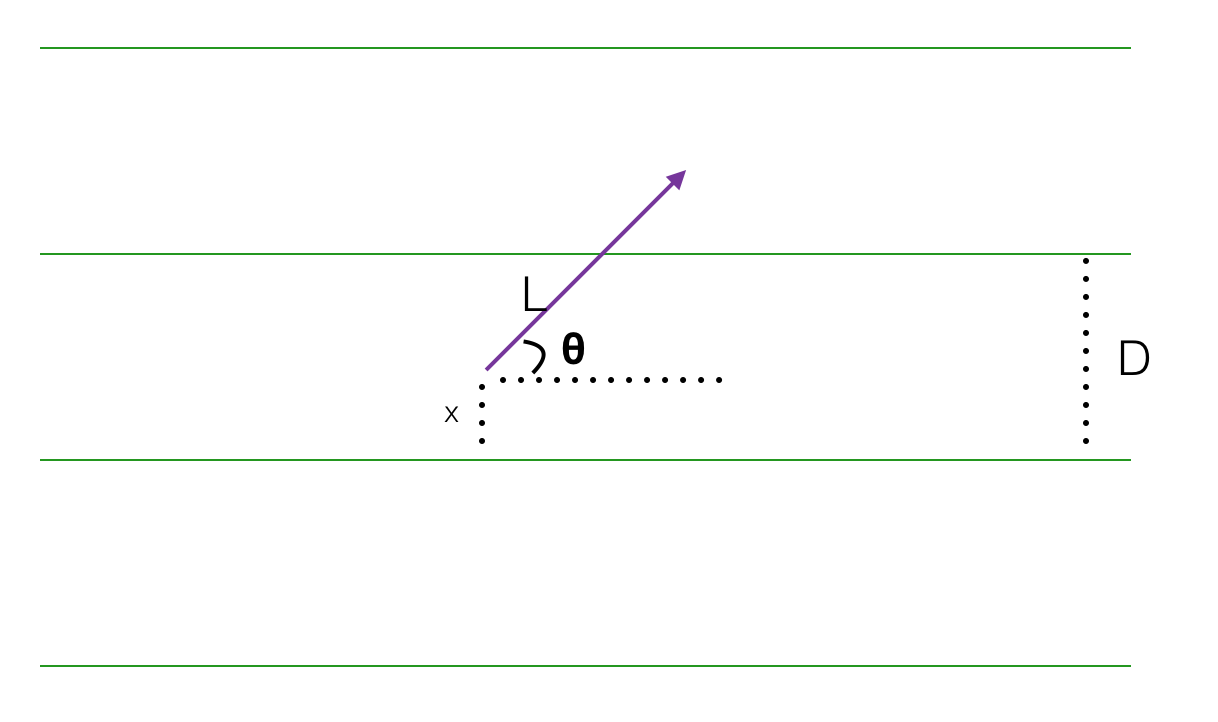
我们很显然就可以得出一个判断条件,即如果\(D<x + Lsin(\theta)\)的话,那么针就与平行线相交了。即我们找到了这个判断条件。
从两个公式中我们可以发现,\(L\)和\(D\)都是给定值,而只需要通过计算机随机产生\(x\)和\(\theta\)就行了。因为,在我们真实投针的情况中,针长\(L\)和平行间距\(D\)也同样给定值,而我们每扔出一次针,\(x\)和\(\theta\)都是随机产生的。这里想要说明的是,计算机中随机产生的值,并不能真正像我们随机扔针那么随机。而是一种伪随机算法,这个在这里先不多说。好了,所有的食料都准备好了,现在开始下锅。
buffon <- function(n, l, d) # 产生n个随机数, 设定针长l, 平行线间距d
{
x <- runif(n, 0, d) # 随机产生n个从针到平行线底部的距离x
theta <- runif(n, 0, pi) # 随机产生n个夹角theta
dis <- x + l*sin(theta)
inter <- 0 # 设置相交初值
output <- 0
for (i in 1:n)
{
if (d < dis[i]) inter = inter + 1 # 计算相交次数
output[i] = inter
}
output
}
stored <- buffon(3000, 1, 1) # 开始试验,每一场做3000次,l = 1, d = 1
estimate_pi <- 0
for (i in 1:3000)
{
estimate_pi[i] <- 2/(stored[i]/i) #计算每一场试验的pi
}
出来的结果:
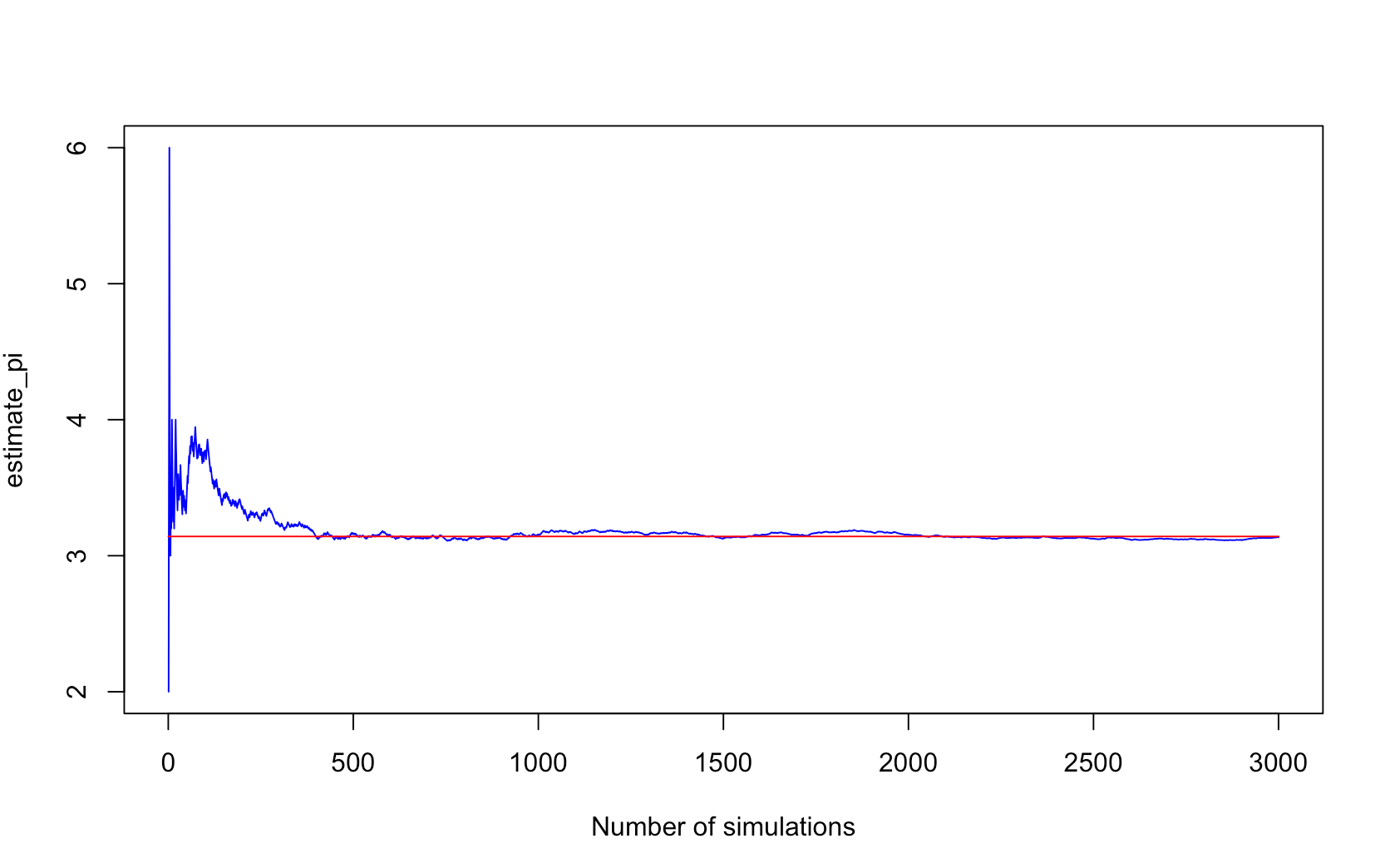
红色的线是计算机里面的真实\(\pi\)值,蓝色的为模拟的,效果还不错。